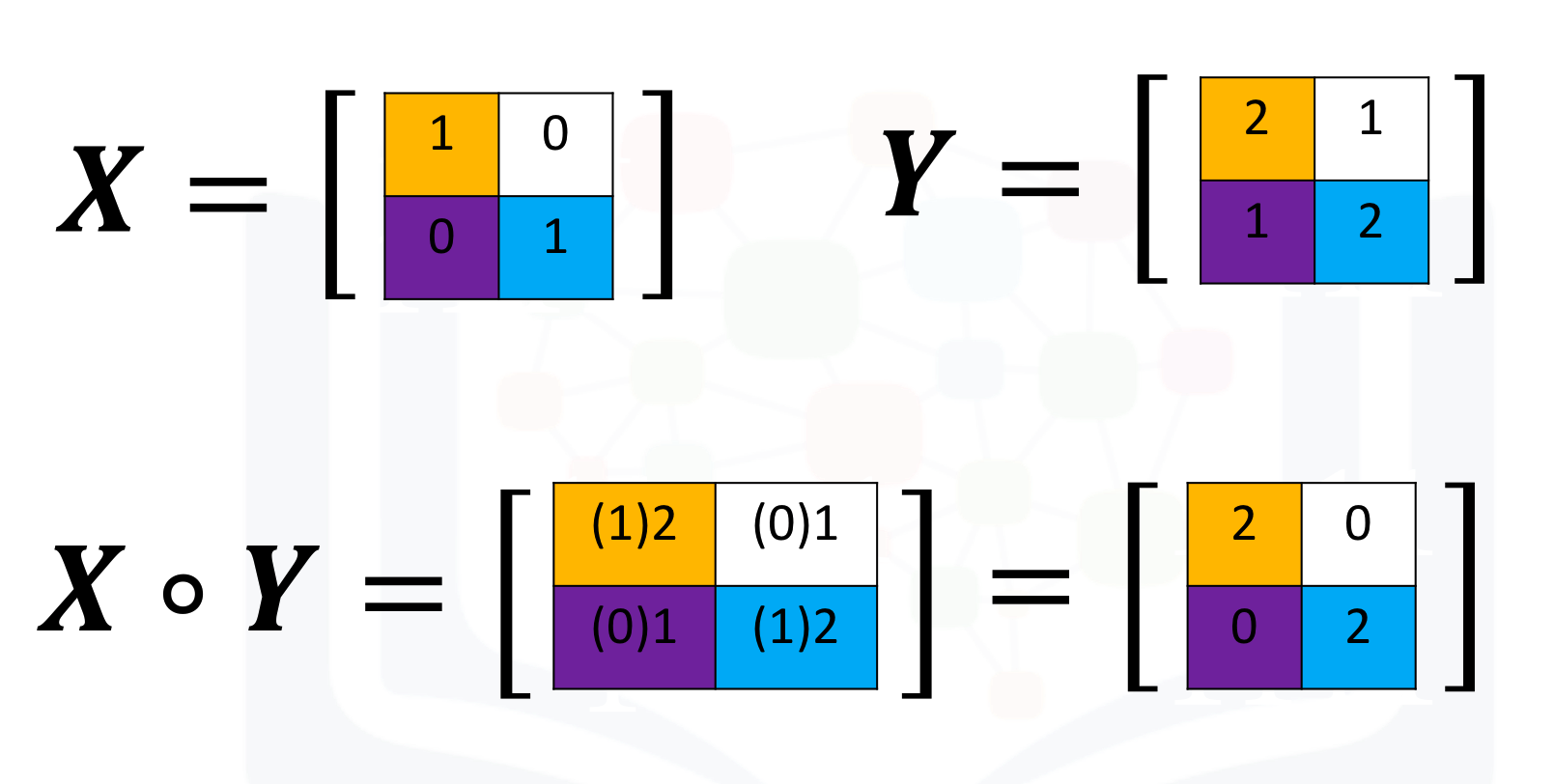# These are the libraries will be used for this lab.
import numpy as np
import matplotlib.pyplot as plt
import torch
import pandas as pdTorch Tensors in 2D

Two-Dimensional Tensors
Objective
- How to perform tensor operations on 2D tensors.
Table of Contents
In this lab, you will learn the basics of tensor operations on 2D tensors.
Estimated Time Needed: 10 min
Preparation
The following are the libraries we are going to use for this lab.
Types and Shape
The methods and types for 2D tensors is similar to the methods and types for 1D tensors which has been introduced in Previous Lab.
Let us see how to convert a 2D list to a 2D tensor. First, let us create a 3X3 2D tensor. Then let us try to use torch.tensor() which we used for converting a 1D list to 1D tensor. Is it going to work?
# Convert 2D List to 2D Tensor
twoD_list = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
twoD_tensor = torch.tensor(twoD_list)
print("The New 2D Tensor: ", twoD_tensor)Bravo! The method torch.tensor() works perfectly.Now, let us try other functions we studied in the Previous Lab.
Let us try tensor_obj.ndimension() (tensor_obj: This can be any tensor object), tensor_obj.shape, and tensor_obj.size()
# Try tensor_obj.ndimension(), tensor_obj.shape, tensor_obj.size()
print("The dimension of twoD_tensor: ", twoD_tensor.ndimension())
print("The shape of twoD_tensor: ", twoD_tensor.shape)
print("The shape of twoD_tensor: ", twoD_tensor.size())
print("The number of elements in twoD_tensor: ", twoD_tensor.numel())Because it is a 2D 3X3 tensor, the outputs are correct.
Now, let us try converting the tensor to a numpy array and convert the numpy array back to a tensor.
# Convert tensor to numpy array; Convert numpy array to tensor
twoD_numpy = twoD_tensor.numpy()
print("Tensor -> Numpy Array:")
print("The numpy array after converting: ", twoD_numpy)
print("Type after converting: ", twoD_numpy.dtype)
print("================================================")
new_twoD_tensor = torch.from_numpy(twoD_numpy)
print("Numpy Array -> Tensor:")
print("The tensor after converting:", new_twoD_tensor)
print("Type after converting: ", new_twoD_tensor.dtype)The result shows the tensor has successfully been converted to a numpy array and then converted back to a tensor.
Now let us try to convert a Pandas Dataframe to a tensor. The process is the Same as the 1D conversion, we can obtain the numpy array via the attribute values. Then, we can use torch.from_numpy() to convert the value of the Pandas Series to a tensor.
# Try to convert the Panda Dataframe to tensor
df = pd.DataFrame({'a':[11,21,31],'b':[12,22,312]})
print("Pandas Dataframe to numpy: ", df.values)
print("Type BEFORE converting: ", df.values.dtype)
print("================================================")
new_tensor = torch.from_numpy(df.values)
print("Tensor AFTER converting: ", new_tensor)
print("Type AFTER converting: ", new_tensor.dtype)Practice
Try to convert the following Pandas Dataframe to a tensor
# Practice: try to convert Pandas Series to tensor
df = pd.DataFrame({'A':[11, 33, 22],'B':[3, 3, 2]})Double-click here for the solution.
Indexing and Slicing
You can use rectangular brackets to access the different elements of the tensor. The correspondence between the rectangular brackets and the list and the rectangular representation is shown in the following figure for a 3X3 tensor:

You can access the 2nd-row 3rd-column as shown in the following figure:
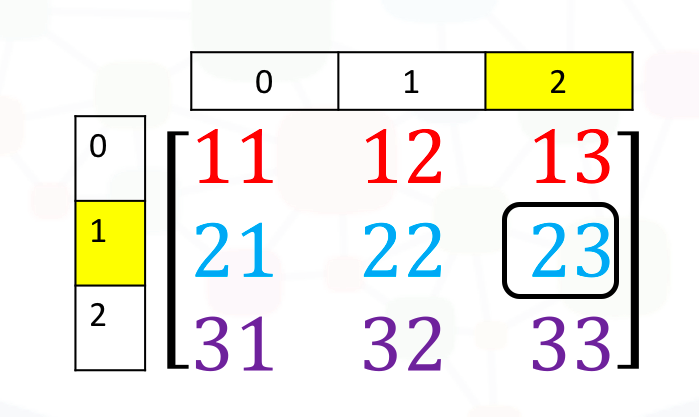
You simply use the square brackets and the indices corresponding to the element that you want.
Now, let us try to access the value on position 2nd-row 3rd-column. Remember that the index is always 1 less than how we count rows and columns. There are two ways to access the certain value of a tensor. The example in code will be the same as the example picture above.
# Use tensor_obj[row, column] and tensor_obj[row][column] to access certain position
tensor_example = torch.tensor([[11, 12, 13], [21, 22, 23], [31, 32, 33]])
print("What is the value on 2nd-row 3rd-column? ", tensor_example[1, 2])
print("What is the value on 2nd-row 3rd-column? ", tensor_example[1][2])As we can see, both methods return the true value (the same value as the picture above). Therefore, both of the methods work.
Consider the elements shown in the following figure:
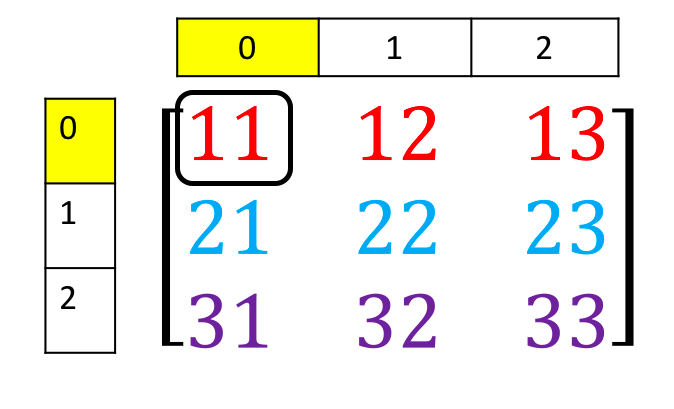
Use the method above, we can access the 1st-row 1st-column by tensor_example[0][0]
tensor_example[0][0]But what if we want to get the value on both 1st-row 1st-column and 1st-row 2nd-column?
You can also use slicing in a tensor. Consider the following figure. You want to obtain the 1st two columns in the 1st row:
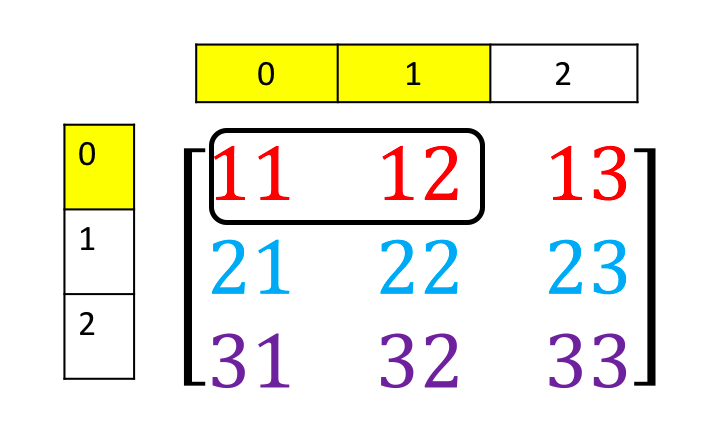
Let us see how we use slicing with 2D tensors to get the values in the above picture.
# Use tensor_obj[begin_row_number: end_row_number, begin_column_number: end_column number]
# and tensor_obj[row][begin_column_number: end_column number] to do the slicing
tensor_example = torch.tensor([[11, 12, 13], [21, 22, 23], [31, 32, 33]])
print("What is the value on 1st-row first two columns? ", tensor_example[0, 0:2])
print("What is the value on 1st-row first two columns? ", tensor_example[0][0:2])We get the result as tensor([11, 12]) successfully.
But we can’t combine using slicing on row and pick one column by using the code tensor_obj[begin_row_number: end_row_number][begin_column_number: end_column number]. The reason is that the slicing will be applied on the tensor first. The result type will be a two dimension again. The second bracket will no longer represent the index of the column it will be the index of the row at that time. Let us see an example.
# Give an idea on tensor_obj[number: number][number]
tensor_example = torch.tensor([[11, 12, 13], [21, 22, 23], [31, 32, 33]])
sliced_tensor_example = tensor_example[1:3]
print("1. Slicing step on tensor_example: ")
print("Result after tensor_example[1:3]: ", sliced_tensor_example)
print("Dimension after tensor_example[1:3]: ", sliced_tensor_example.ndimension())
print("================================================")
print("2. Pick an index on sliced_tensor_example: ")
print("Result after sliced_tensor_example[1]: ", sliced_tensor_example[1])
print("Dimension after sliced_tensor_example[1]: ", sliced_tensor_example[1].ndimension())
print("================================================")
print("3. Combine these step together:")
print("Result: ", tensor_example[1:3][1])
print("Dimension: ", tensor_example[1:3][1].ndimension())See the results and dimensions in 2 and 3 are the same. Both of them contains the 3rd row in the tensor_example, but not the last two values in the 3rd column.
So how can we get the elements in the 3rd column with the last two rows? As the below picture.
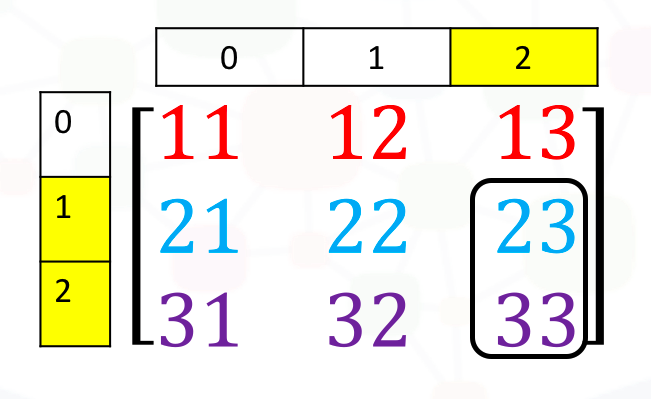
Let’s see the code below.
# Use tensor_obj[begin_row_number: end_row_number, begin_column_number: end_column number]
tensor_example = torch.tensor([[11, 12, 13], [21, 22, 23], [31, 32, 33]])
print("What is the value on 3rd-column last two rows? ", tensor_example[1:3, 2])Fortunately, the code tensor_obj[begin_row_number: end_row_number, begin_column_number: end_column number] is still works.
Practice
Try to change the values on the second column and the last two rows to 0. Basically, change the values on tensor_ques[1][1] and tensor_ques[2][1] to 0.
# Practice: Use slice and index to change the values on the matrix tensor_ques.
tensor_ques = torch.tensor([[11, 12, 13], [21, 22, 23], [31, 32, 33]])Double-click here for the solution.
Tensor Operations
We can also do some calculations on 2D tensors.
Tensor Addition
You can also add tensors; the process is identical to matrix addition. Matrix addition of X and Y is shown in the following figure:
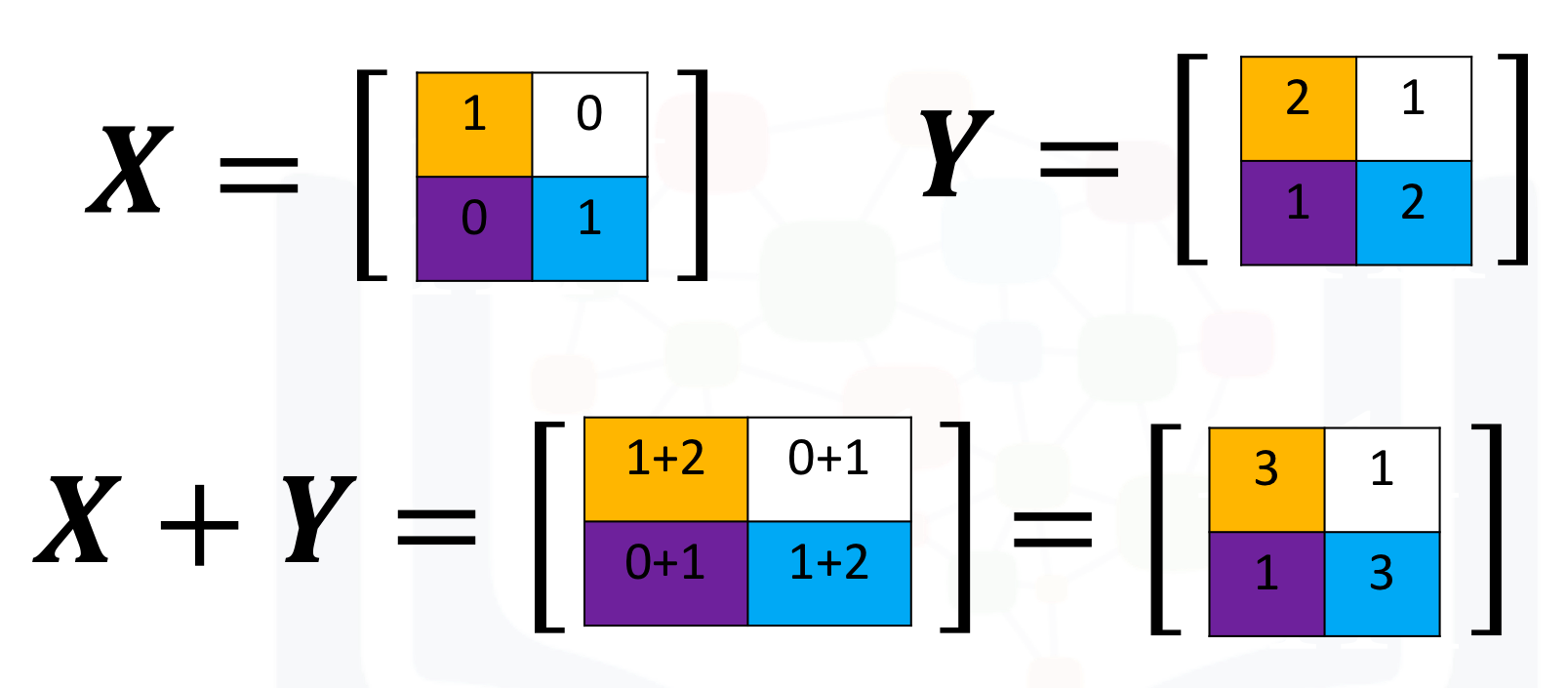
Let us see how tensor addition works with X and Y.
# Calculate [[1, 0], [0, 1]] + [[2, 1], [1, 2]]
X = torch.tensor([[1, 0],[0, 1]])
Y = torch.tensor([[2, 1],[1, 2]])
X_plus_Y = X + Y
print("The result of X + Y: ", X_plus_Y)Like the result shown in the picture above. The result is [[3, 1], [1, 3]]
Scalar Multiplication
Multiplying a tensor by a scalar is identical to multiplying a matrix by a scaler. If you multiply the matrix Y by the scalar 2, you simply multiply every element in the matrix by 2 as shown in the figure:
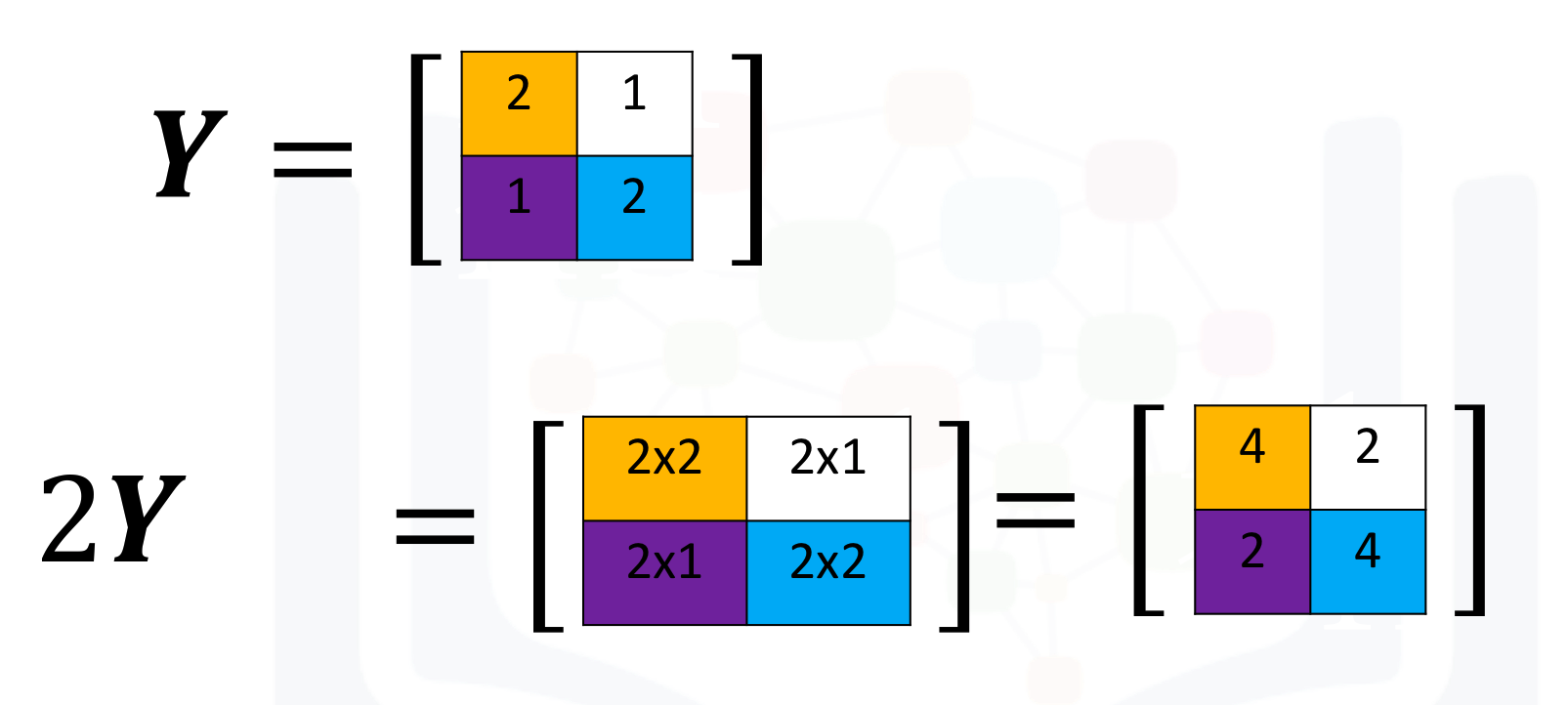
Let us try to calculate the product of 2Y.
# Calculate 2 * [[2, 1], [1, 2]]
Y = torch.tensor([[2, 1], [1, 2]])
two_Y = 2 * Y
print("The result of 2Y: ", two_Y)Element-wise Product/Hadamard Product
Multiplication of two tensors corresponds to an element-wise product or Hadamard product. Consider matrix the X and Y with the same size. The Hadamard product corresponds to multiplying each of the elements at the same position, that is, multiplying elements with the same color together. The result is a new matrix that is the same size as matrix X and Y as shown in the following figure:
The code below calculates the element-wise product of the tensor X and Y:
# Calculate [[1, 0], [0, 1]] * [[2, 1], [1, 2]]
X = torch.tensor([[1, 0], [0, 1]])
Y = torch.tensor([[2, 1], [1, 2]])
X_times_Y = X * Y
print("The result of X * Y: ", X_times_Y)This is a simple calculation. The result from the code matches the result shown in the picture.
Matrix Multiplication
We can also apply matrix multiplication to two tensors, if you have learned linear algebra, you should know that in the multiplication of two matrices order matters. This means if X * Y is valid, it does not mean Y * X is valid. The number of columns of the matrix on the left side of the multiplication sign must equal to the number of rows of the matrix on the right side.
First, let us create a tensor X with size 2X3. Then, let us create another tensor Y with size 3X2. Since the number of columns of X is equal to the number of rows of Y. We are able to perform the multiplication.
We use torch.mm() for calculating the multiplication between tensors with different sizes.
# Calculate [[0, 1, 1], [1, 0, 1]] * [[1, 1], [1, 1], [-1, 1]]
A = torch.tensor([[0, 1, 1], [1, 0, 1]])
B = torch.tensor([[1, 1], [1, 1], [-1, 1]])
A_times_B = torch.mm(A,B)
print("The result of A * B: ", A_times_B)Practice
Try to create your own two tensors (X and Y) with different sizes, and multiply them.
# Practice: Calculate the product of two tensors (X and Y) with different sizes
# Type your code here